도형 中 '삼각형, 사각형, 원' 관련 표현들 - 영어로는?
지난번 도형과 관련된 가장 기본적인 표현들에 이어서(하단 링크 참조)
이번에는 서로 다른 종류의 삼각형/사각형/원의 영어 표현에 대해서 다뤄본다.

우선 삼각형은 영어로 triangle.
별다른 설명은 필요가 없지 않을까 싶다.
굳이 파고들자면 triangle이란 단어는 tri + angle 이 합쳐진 단어로,
'3'을 뜻하는 'tri'와 '각'을 뜻하는 'angle'이 합쳐진 단어다.
(그렇다고 해서 똑같은 논리로 각각의 접두사가 붙어서,
사각형은 quadrangle이고 오각형은 pentangle, 육각형은 hexangle 계속 이렇게 이어지냐,라고 묻는다면
영어가 웃긴게 또 그렇지는 않다. (사각형-quadrangle 여기까지는 맞긴 하지만.)
이거는 아마 다음 글에서 다룰 것 같다.)
여기서 세부적으로 들어가서,
우선 정삼각형(위의 이미지가 정삼각형이다)은 영어로?
의외로 잘 안 쓰이는 단어라서 아는 분이 많지 않을 것이다.
정삼각형은 영어로 'regular triangle 또는 'equilateral triangle'이라고 한다.
'regular'가 붙은 것은, regular라는 단어가 가진 수많은 의미 중, '균형 잡힌'이라는 의미에서 나온 것일 것이다.
각각의 변의 길이, 각도 모든 게 똑같이 균형 잡혔으니까.
'equilateral'의 경우, equi + lateral이 합쳐진 것인데, 'equi'는 '동일한, 동등한'이라는 의미,
(참고로, equal이라는 단어가 여기서 파생된 것이다.)
그리고 'lateral'의 경우 일반적으로는 '옆의, 측면의' 정도로만 알고 있지만, 라틴어에서 유래된 이것의 본래 의미는
'belonging to the side' 즉, (측)'면'과 관련된, 이라는 뜻이다.
즉 '모든 '면'(또는 '변')이 동일한' 이라는 뜻이 되겠다.
그래서 'equilateral triangle = 정삼각형'이 되는 것이다.
일상적으로는 'regular'를 붙인 표현을 더 많이 쓴다고 느낀다.
단어의 register 차이가 워낙 심해서, 당연하다면 당연하겠지만.

다음은 이등변삼각형.
우리말로 하면 이+등변+삼각형, 즉, '두 개의 같은 길이의 변을 가진 삼각형'이라서, 바로 와닿는 표현이다.
그런데 이게 꽤나 어려운 단어다.
이등변 삼각형은 영어로 'isosceles triangle'이라고 한다.
그러면 우리말의 '이등변'에 대응하는 영어 단어가 'isosceles'라는 뜻인데,
도대체 이게 무슨 말일까?
iso + sceles로 합쳐진 것인데, 여기서의 'iso'는 '동일한, 동등한'이라는 의미
'sceles'는 'leg', 즉 '다리'라는 의미이다.
그런데 잠깐 생각해보면 좀 이상할 수 있는 게,
아까 위에 정삼각형 설명할 때 'equi' 부분이 '동일한, 동등한'이라는 뜻을 가진 부분이라고 했다.
거기서 'equal'이라는 단어도 나온 거고.
그런데 'iso'는? - 이건 왜 그런 거냐면,
'equi' - 이건 라틴어에서 나온 말이고, 'iso' - 이건 그리스어에서 나온 말이기 때문이다.
얼마 전 썼던 multi- / poly- 와 본질적으로 같은 케이스라고 보면 된다.
그러면 다시 'sceles'로 넘어가서, 이게 'leg'라는 뜻인데,
그러면 '다리가 같은'이라는 뜻이 된다.
이등변 삼각형이 뭔지 알고 있는 상태니까, 여기서 말하는 '다리'가 뭔진 알겠는데,
근데 진짜로 영어에서 이걸 'leg'라고 쓰나?라고 묻는다면 진짜로 쓴다. 아래와 같이 말이다.

이등변 삼각형의 세 변 중, 아래의 밑변을 'base'라고 한다면, 나머지 길이가 같은 2개의 변을 실제로
'leg'라고 부른다.
뭐 셋 다 그냥 'side'라고 불러도 무방하겠지만, 이등변삼각형의 특징 상,
한 개의 base와 두 개의 leg로 구성되어있다고 표현할 수 있을 것이다.
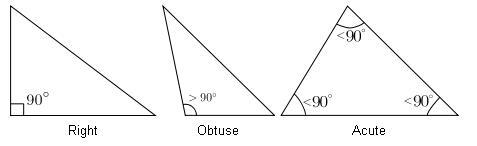
마지막으로 직각삼각형 / 예각 삼각형 / 둔각 삼각형 세트다.
지난번 글에서 다룬 직각/예각/삼각을 그대로 적용시키면 되는, 아주 간단한 케이스다.
직각삼각형: right triangle, 또는 right-angled triangle (둘 다 맞는 말이며, 스타일의 차이일 뿐이다.)
예각 삼각형: acute triangle, 또는 acute-angled triangle (마찬가지.)
둔각 삼각형: obtuse triangle, 또는 obtuse-angled triangle (마찬가지.)

다음 사각형으로 넘어간다.
우선, 삼각형이 triangle이라는 건 대부분 알겠지만,
'사각형'이 뭐냐고 한다면 십중팔구는 square라는 답이 나올 것이다.
그리고 나머지는 아마 rectangle 정도가 나오지 않을까 싶다.
일반적인 쓰임으로는 당연히 다 맞겠지만, 엄밀히 따지자면
'사각형'은 영어로 quadrilateral 또는 quadrangle이다.
아마 의외일 것이다. 생각보다 어려운 느낌이라서..
아까 삼각형 부분에서 다 설명한 부분이기 때문에, qudri-, qudra-가 '4'를 뜻한다는 것만 설명하면
그 외는 따로 추가적인 설명은 필요가 없어 보이긴 한다.
그러면 제일 일반적으로 말하는 'square'는 정확히 뭘까?
바로 '정사각형'이라는 뜻이다. (위의 이미지가 정사각형이다.)
네 변의 길이도 같고, 각도 각각 90도로 같은 것만을 'square'라고 정의한다.

다음은 직사각형.
흔히들 알고 있겠지만, 직사각형은 영어로 rectangle이라고 한다.
이것도 어원만 간략히 설명하자면 'rect' 부분이 라틴어의 'rectus', 즉 ' right, straight'을 뜻하는 말에서
나온 것이다. 이제 자주 나와서, right이라는 표현에서 유추할 수 있듯,
각각의 각도가 90도인 사각형을 일컫는다고 보면 되겠다.

다음은 사다리꼴.
사다리꼴은 영어로 'trapezoid'라고 한다.
어원은 옛날 그리스어 'trapeza'로 테이블 내지는 네 개의 발,다리/각을 뜻하는 말에서 나왔다고 하는데,
별로 와닿지 않는 어원에 설명이고, 위의 다른 표현과 같이 다른 영어단어 공부에 도움이 될 것 같은
어원 자체가 아니라고 판단해서 얘는 그냥 생략하겠다.

**2023.3.21 수정:
trapezoid가 '사다리꼴'임을 설명하는 데에 이 어원은 크게 도움이 안 되지만,
2023년 3월 21일 인체의 여러 근육 이름 중 '승모근'에 대해 다루는 중에 이 어원이 어느 정도는 도움이 될 수도 있겠다는 생각이 들었다.
(해당 글의 링크에서 이 글로 온 분은 다른 도형들의 영어 표현도 한 번 훑어보고 가시면 도움이 될 것 같다.)
다음은 평행사변형.
평행사변형은 영어로 'parallelogram'이라고 한다.
지난번 글에서 '평행-parallel'에 대해서 한 번 다룬 적이 있기 때문에, 이 단어는 쉽게 와닿을 것이라고 생각한다.
유래를 따지자면, 그리스어 'parállēlos'와 'grammḗ'이 합쳐진 것인데, 앞부분은 단어 생긴 것을 보면 알 수 있듯, 역시 '평행'이라는 뜻이고, 뒤의 'grammḗ' 부분은 영어로 'line'이라는 뜻이다. 굉장히 직관적이다.
평행사변형에서 마주 보는 각 변들이(line이) 서로 평행하니까, 그 정의와 함께 쉽게 유추할 수 있는 부분이다.
마지막으로 마름모.
마름모는 영어로 'rhombus'라고 한다.
마찬가지로 옛 그리스어 'rhómbos'에서 유래된 단어이고, 그 뜻은 'spinning top, 즉, 돌고 있는 팽이'
라는 뜻이라고 한다. 아래와 같이 말이다.

아닌 게 아니라, 실제로 비슷하게 생겼다. (비록 위의 팽이를 포함한 많은 팽이들이 마름모의 정의에 정확히 부합하지는 않지만, 우리가 흔히 말하는 '마름모꼴'은 맞으니까.)

원은 영어로 circle이다.
이건 별다른 설명이 필요 없을 것 같다.
모르는 사람도 거의 없을 것이라 생각한다.

마지막으로 타원이다.
타원은 영어로 'ellipse'라고 한다.
그런데 타원이라고 하면 아마 꽤 많은 사람들이 ellipse보다 'oval'이라는 단어가 먼저 떠오를 것이다.
하지만 이 둘은 엄밀히 말하면, 구별이 된다.

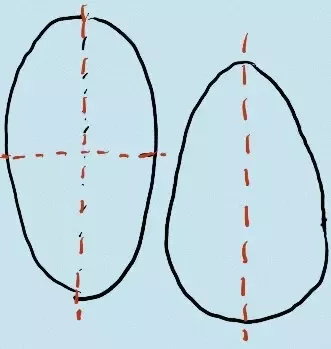
위 사진에서 보듯, 왼쪽이 ellipse이고, 오른쪽이 oval이다.
뭐가 다른 거지??라고 묻는다면, 아래의 원어민의 의견을 사진과 함께 한번 보길 바란다.
"There is no precise definition of an oval in mathematics.
It is said to resemble the outer of an egg.
The one on the left is an ellipse and on the right is an oval.
Ellipse is a mathematically defined shape whereas an oval is not so.
An ellipse has at least two axes of symmetry
but an oval has at least one.
One can easily say that an oval is a precursor of an ellipse. It looks like an uneven circle or a circle which is squeezed from two sides.
All ellipses are ovals but all ovals are not ellipses."
-즉, 선이 그어진 사진을 보면 알 수 있듯,
ellipse = 위아래로 나눠도, 좌우로 나눠도 대칭이 됨(엄격한 의미에서의 '타원'의 개념)
oval = 위아래든, 좌우든 최소 한쪽으로만 대칭이 되면 됨 (널널한 의미에서의 '타원'의 개념으로 볼 수 있음)
oval의 경우, 더욱더 널널하게 정의를 하자면 (대칭과는 무관하게) '알과 비슷한 형체의 무언가'는 그냥
oval이라고 할 수 있다.
애초에 'oval'이라는 단어 자체가 '알'을 뜻하는 라틴어 'ovum'이라는 단어에서 나온 것이다.

타원을 뜻하는 ellipse는 명확한 수학적 '정의'가 있는 반면,
oval은 사실 수학적으로 정의된 바가 없는 단어라는 점이 결국 핵심이다.
하지만, 수학적/기하학적으로 따지지 않았을 때,
그냥 일상생활에서는 그냥 ellipse나 oval이나 그게 그거라고 보고 사용해도 별 문제는 없을 것이다.
(이런거 하나하나 너무 깊게 따지면 피곤한 것도 사실이다.)
하지만 적어도 알고는 있으면 도움이 될 것이다.
다음 글에서는 다각형(polygon) 전반에 대해 다뤄본다.
지난 글 링크:
'도형' 관련 표현들 -점, 선(직선, 곡선, 대각선), 넓이, 각도(직각, 예각, 둔각), 평행, 수직) 등등.. - 영어로는?
https://speckofdust.tistory.com/55
'도형' 관련 표현들 -점, 선(직선, 곡선, 대각선), 넓이, 각도(직각, 예각, 둔각), 평행, 수직) 등등..
'도형' 관련 표현들 - 영어로 이번에는 도형, 특히 수학 시간에 배우는 개념의 도형에 관한 여러 가지 표현들을 영어로 어떻게 표현하는지에 대해 다뤄본다. 크게 '도형' 그 자체에서부터 시작
speckofdust.tistory.com
'영어 관련 지식 > 수학' 카테고리의 다른 글
| '원' 관련 표현 영어로- 중심, 지름, 반지름, 둘레 (0) | 2022.02.16 |
|---|---|
| '입체도형' (구, 원기둥, 원뿔, 각뿔, 각기둥, 직육면체, 정육면체 / 부피) - 영어로 (0) | 2022.02.13 |
| '다각형' (삼각형, 사각형, 오각형, 육각형 등등..) - 영어로 (1) | 2022.02.10 |
| '도형' 관련 표현들 -점, 선(직선, 곡선, 대각선), 넓이, 각도(직각, 예각, 둔각), 평행, 수직) 등등.. - 영어로는? (0) | 2022.02.06 |
| '질량(무게)' 단위 영어 표현 - 온스(ounce), 파운드(pound) (0) | 2022.02.02 |
| '부피' 단위 영어 표현 - 온스(ounce), 파인트(pint), 쿼트(quart), 갤런(gallon) (0) | 2022.02.01 |




댓글